Skip to main content

Comparison between Logistic Regression and Support Vector Machine


Logistic regression and support vector machine (SVM) are both popular models that can be applied to classification tasks. This article gives the introduction of these two methods and summarizes the differences between them.

What is Logistic Regression?

Logistic regression is a generalized linear model for binary classification. In logistic regression, we take the output of the linear function and then pass the value to the sigmoid function. The sigmoid function is S-shaped,  it is a bounded and differentiable activation function.  We use sigmoid function in logistic regression because it can take any real-valued number and map it into a value between the range of 0 and 1, as is known to all, the probability of any event is between 0 and 1, so sigmoid function is an intuitive and right choice for logistic regression. After we get the probabilities, we then set a threshold to make decisions, if the probability is greater than the threshold, we assign it a label 1, else we assign it a label 0.


Image source: https://www.saedsayad.com/images/LogReg_1.png


What is Support Vector Machine (SVM)?

A support vector machine makes classifications by using the hinge loss function to find the optimal hyperplane that maximizes the margin between the classes. Data points falling on either side of the hyperplane can be attributed to different classes. 

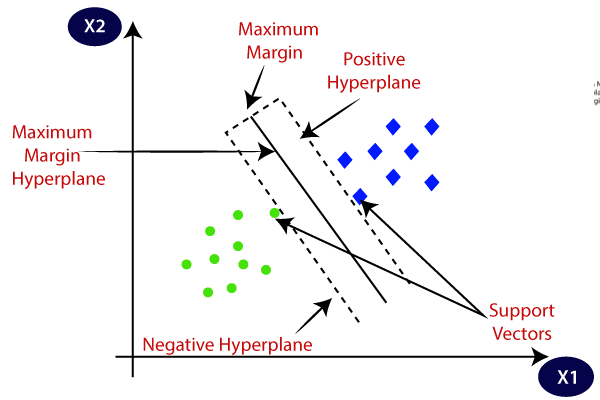
Support Vector Machine (SVM) Algorithm - Javatpoint
https://static.javatpoint.com/tutorial/machine-learning/images/support-vector-machine-algorithm.png


What's the difference between logistic regression and support vector machine?

  • They are different in loss function. Logistic regression minimize log loss function while SVM minimizes hinge loss function.
Log loss function
Hinge loss function

  • When we have a perfect linearly separable dataset, SVM can easily find the optimal hyperplane and all the data points can be classified correctly, while logistic regression will have difficulty to converge, thus failing to make classifications.
  • Logistic regression is more sensitive to outliers than SVM. 
    • Because logistic  regression finds its boundary by including all the data, so some outliers can make a difference to the boundary. 
    • SVM finds its maximal margin hyperplane by several support vectors that lie along the lines indicating the width of the maximal margin, so outliers that are far away from the margin have no effects on its decision boundary.
  • SVM do not directly provide probabilities (values between 0 and 1), while logistic regression can easily produce probabilities. 
    • This might be a good property for logistic regression when what we want is an estimation, instead of absolute predictions, or when we don't have enough confidence into the data.
  • SVM is more flexible than logistic regression.
    • With different kernels (RBF, POLY, etc), SVM can learn different patterns in a non-linear dataset, however, it can be tricky to find the most appropriate kernel sometimes. 
    • Logistic regression assumes linearity between the log odds of an event occurring and predictor variables, so it may not perform well when we have a complex non-linear dataset.
  • SVM woks better for high dimensional data.
    • SVM is computationally efficient (with kernel tricks), especially when working with higher dimensional spaces.
  • SVM works well with unstructured and semi-structured data (like text and images), while logistic regression works with already identified independent variables.



Comments

Post a Comment

Popular posts from this blog

Use Monte Carlo Simulation + Hypothesis Test to Evaluate Missing Value Imputation

It is quite normal that there’s a lot of missing values here and there when you get a dataset in the real world. How to deal with missing values is a big topic. As far as I’m concerned, there’s no one optimal method that works for all situations, usually, it is case-by-case.  For me, most of the time I don’t want to throw away observations that contains missing values, unless the data is really large while the missing value percentage under certain features are quite high (e.g. >98%) and those features do not play an important role in the analysis. Otherwise I’ll try my best to impute all the missing values to retain important information in the data as much as possible. There’s a lot of missing value imputation methods out there, including statistical methods and machine learning methods. No matter what method we use, we want a data distribution (after imputation) that is not twisted, or in other words, is not statistically significantly different from the original distribution...
Post a Comment
Read more

Use Flowers to Analyze PCA and NMF

PCA and NMF are both dimension reduction methods that can be used for BIG DATA  problems. They use matrix algebra to transform the original feature space in the dataset to a much lower dimensional space while keeping the majority of the information in the dataset. To make this article more vivid, I would like to use image data to show the functionality and difference about these two methods. In fact, PCA and NMF are very natural transformation methods for image data, because image data has large feature space (width x height x channel) and pixels in the image are also highly correlated. Let’s take a look at this flower dataset first. The flower data set I used in this article was from Kaggle ( https://www.kaggle.com/alxmamaev/flowers-recognition ) We have roses and sunflowers in this image dataset. Each image is represented as a 128x128x3 numpy array. So if you flatten each image, you will get a 1D array with 49152 features, which is a REALLY LARGE number in terms of features....
Post a Comment
Read more

Why Do We Need Precision-Recall Curve?

  What are the precision & recall and why are they used?  For binary classification problems, it's usually a matter of how to differentiate from a negative class to a positive class. When we have a binary classifier to make predictions, there will always be true positives (TP) , false positives (FP) , true negatives (TN) , and false negatives (FN) . The classifier that can produce more true positives and negatives (less false positives and negatives in other words) indicates better predictive power and less business cost. As a data scientist, I usually first define the cost of a false negative and the cost of a false positive from a business standpoint, so that I can optimize the threshold accordingly and balance the trade-off. In a nutshell, both precision and recall are the metrics to evaluate the predictive performance. Below are the detailed definitions about precision and recall. precision = TP/(TP + FP) , it tells how sure you are of your true positives. For exa...
1 comment
Read more